What is a TH-pentagon?
A tiling is monohedral if all tiles in the tiling are of the same size and shape. Here, a convex pentagon that can generate a monohedral tiling is called a convex pentagonal tile. At present, essentially 15 families of different types of convex pentagonal tiles are known, but it is not known whether this list is complete. In 1995, Marjorie Rice discovered an interesting tessellation by using convex pentagons. The convex pentagon which Rice used in the discovery belongs to both Type 1 and Type 5 of the known types for convex pentagonal tiles (see Figure 1).
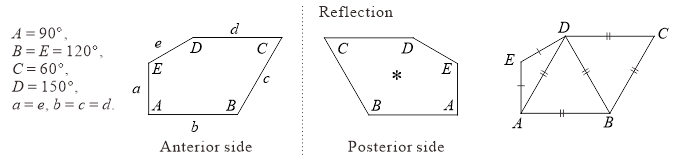
Convex pentagons in Figure 1 can be divided into two equilateral triangles ABD and BCD, and an isosceles triangle ADE. The area of isosceles triangle ADE is equal to 1/3 of the area of equilateral triangle ABD. That is, the convex pentagons in Figure 1 include 7/3 equilateral triangles. The convex pentagon in Figure 1 can be considered as a unique convex pentagon obtained from a trisected heptiamond. (A polyiamond is a plane figure constructed by congruent equilateral triangle joined edge-to-edge. A polyiamond with seven equilateral triangles is called a heptiamond or 7-iamonds. There are 24 unique pieces.)
Hereafter, the convex pentagon of Figure 1 is referred to as a TH-pentagon.
It seems that a tiling of Type 5 and a tiling of Rice that are formed by using the convex pentagonal tile are different patterns. In fact, the tiling of Type 5 and the tiling of Rice can be generated by the difference in the contiguity method of 18 sided polygon (hexagonal flower) that is formed by the TH-pentagon. I found novel properties of the TH-pentagon and many new convex pentagon tilings (tessellations).
Contents
Below, I present the investigated results and the artworks of TH-pentagon. For each content, please click the following link.
• Paper I: "Convex Pentagon Tilings and Heptiamonds, I" (Last update 28/12/2019)
• Paper II: "Convex Pentagon Tilings and Heptiamonds, II" (Last update 28/12/2019)
• Discovered new tilings, I (01/04/2017) (Last update 02/05/2017)
• Discovered new tilings, II (02/05/2017) (Last update 02/05/2017)
• Gallery: Artworks of Tiling by TH-pentagon (Last update 13/10/2021)
• Model (Puzzle) (Last update 09/03/2018)
• Tilings with TH-pentagon and other polygon
