凸五角形タイル張り問題

凸多角形による平面のタイル張り（タイル貼り，タイリング，テセレーション，敷きつめ，tiling, tessellation）研究において，一種類の合同図形のみのでタイル張り可能な凸多角形タイル（平面充填形）の網羅（分類）を目指す問題があります．

内角和が360度を整除できる三角形と四角形（凹も含めて）はすべて多角形タイルで，凸六角形タイルは3つのファミリーに分類でき，7辺以上の凸多角形タイルは存在しないことが知られています（注意：「3種類」でなく「３つのファミリー」としているのは，分類の基準がある固定された形に決めるものではないからです．この3つのファミリーには，それぞれ「Type 1」と「Type 2」と「Type 3」という名前が付いています．したがって「Type 1の凸六角形」とは，「Type 1のファミリーの凸六角形タイル」や「Type 1のファミリーに属する凸六角形タイル」と言う意味です．私はこれまで「Type 1に属す凸六角形タイル」というような表現を用いていますが，上記のような意味合いで使っています．例えば，正六角形はその３つのファミリーにすべてに属します．つまり各Typeのファミリーは互いに素ではないのです）．

凸五角形の充填形のTypeは現在までに，Reinhardt，Richard Brandon Kershner, Richard James Ⅲ, Marjorie Rice, Rolf Stein, Casey Mannらなどによって示された15のファミリーが知られていますが，これで網羅という証明はなく，唯一未解決問題です．この五角形の場合を，凸五角形タイル張り問題と呼びます．注意としては，凸五角形タイル張り問題とは，タイルのTypeのファミリーを分類する問題で，タイルが作る敷きつめ模様を分類するとは違うということです．

凸五角形のタイリングで，凸五角形の辺上に他の凸五角形の頂点を許すような場合は六角形などの凸条件を緩和したタイリングともみなせます．このような観点から，私はタイルの辺が同じ長さの辺のみと接触するようなedge-to-edgeタイル張りが真の意味で充填凸五角形のタイル張りと考え，まずedge-to-edgeタイル張り可能な凸五角形に限定して研究を進めました．

その結果，edge-to-edgeタイル張り可能な凸五角形は，既存の8つのファミリーのTypeのすくなくとも1つに属すことを証明しました（私の論文「Convex Pentagons for Edge-to-Edge Tiling, III」や「Tiling Problem: Convex Pentagons for Edge-to-Edge Monohedral Tiling and Convex Polygons for Aperiodic Tiling」を参照）．

なお15番目のTypeの凸五角形タイルは，2015年にCasey Mannらによって発見されました（発見の連絡は，日本時間だと2015年7月30日にメールで届きました）．14番目の発見から，約30年ぶりの新しいTypeの発見でした．彼らはアイソヘドラル（isohedral）とよばれるタイリングの性質を利用したアイデアを元にコンピュータを使って調査をした結果，Type 15の凸五角形タイルを発見しました（発見当時は，まだ調査の途中で今後さらに見つかるかもしれないとも言っていましたが，その後追加の報告などは届いていません）．

Mannらの論文：http://arxiv.org/abs/1510.011866

ちなみに，上記の表記に従うならばMannらの発見した凸五角形は「Type 15のファミリーに属する凸五角形タイル」となるわけですが，この凸五角形の形はサイズ以外に自由度がありません．つまり，「Type 15のファミリーに属する凸五角形タイル」は1つか存在しないので，まさに「Type 15のファミリーに属する凸五角形タイル」は「Type 15の凸五角形タイル」であると言えます（誤解が生じません）．「Type 14のファミリーに属する凸五角形タイル」も同様な性質とです．

七辺以上の凸多角形タイルが存在しないことの証明は，「M.S. Klamkin and A. Liu, Note on a result of Niven on impossible tessellations, American Mathematical Monthly, 87 (1980) 651--653.」などが参考になります．

凸六角形タイルの3つのファミリーのTypeは，WolframMathWorld"Hexagon Tiling"などで確認できます．

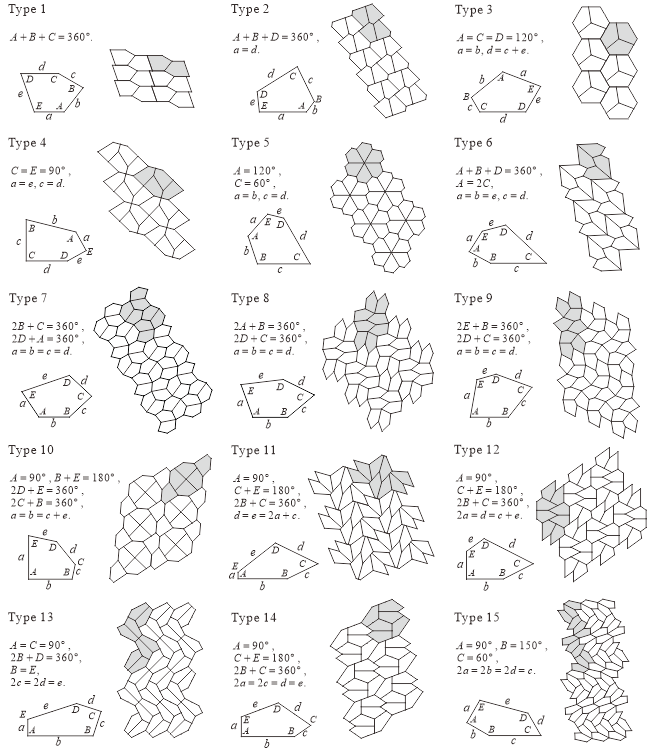
凸五角形タイルの15のファミリーのTypeは，下図やWolframMathWorld"Pentagon Tiling"などで確認できますし，私の各論文などで条件式などを含め確認できます（注意：2016年1月号の数学セミナーの「平面タイル張り可能な凸五角形」の図1には編集による誤植があるので注意してください）．

Edge-to-edgeタイル張り可能な凸五角形タイルが属す8つのファミリーのTypeは，私の論文の「Convex Pentagons for Edge-to-Edge Tiling, III 」と「Tiling Problem: Convex Pentagons for Edge-to-Edge Monohedral Tiling and Convex Polygons for Aperiodic Tiling」などで確認できます．Edge-to-edgeタイル張り可能な凸五角形タイルが属す8つのファミリーのTypeは互いに素ではありません．「すくなくとも1つに属す」という表現がそのことを示唆しています（ただし論文での表記はちょっと違っていて，Remarkで「互いに素でない」と説明をしています）．「Convex Pentagons for Edge-to-Edge Tiling, III 」には，edge-to-edgeタイル張り可能な凸五角形のTypeの集合に関するベン図も示しています．

Heesch数を持つ凸五角形

凸多角形による平面のタイル張り（タイル貼り，タイリング，テセレーション，敷きつめ，tiling, tessellation）研究において，一種類の合同図形のみのでタイル張り可能な凸多角形タイル（平面充填形）の網羅（分類）を目指す問題があります．

Edge-to-edgeタイル張り可能な凸五角形の研究を利用して，Heesch数を持つ凸五角形の調査をしています．Heesch数に関しては，Wikipedia「Heesch's problemを参照してください（注意：2018年10月現在Wikipediaに掲載されている「Ammann's example of a polygon with Heesch number 4」と書かれているのは間違いです．AmmannはHeesch数が3のタイルを見つけましたが，Heesch数が4のタイルは見つけていないと思われます．この図は，一番外側にルールが破綻している箇所があります）．

2005年に広島大学の阿賀岡先生が「An example of convex heptagon with Heesch number one」にてHeesch数が1の凸七角形を発見しました．この論文内で「接続がedge-to-edgeであるような有限のHeesch数を持つ凸五角形は存在するか？」という問題を示していましたが，それに該当する凸五角形を2015年に見つけました．この研究はまだ終わっていませんが，とりあえず1つ論文としてまとめました．この論文で紹介している1つを，2017年にCraig S. Kaplan教授見つけて「Heesch Numbers, Part 4: Edge-to-Edge Pentagons」にて紹介しています．

さて，Heesch数が1の凸五角形ですこし面白いものがあることに気づきました．Heesch数が1の凸五角形ですから，その凸五角形の周りを1回しか囲めないのですが，実うまく配置すると，3個の凸五角形の集団の周りを完全に1回だけ囲むことができるものがいくつかあります．下記の図はその例です（囲み方も1つとは限りません）．

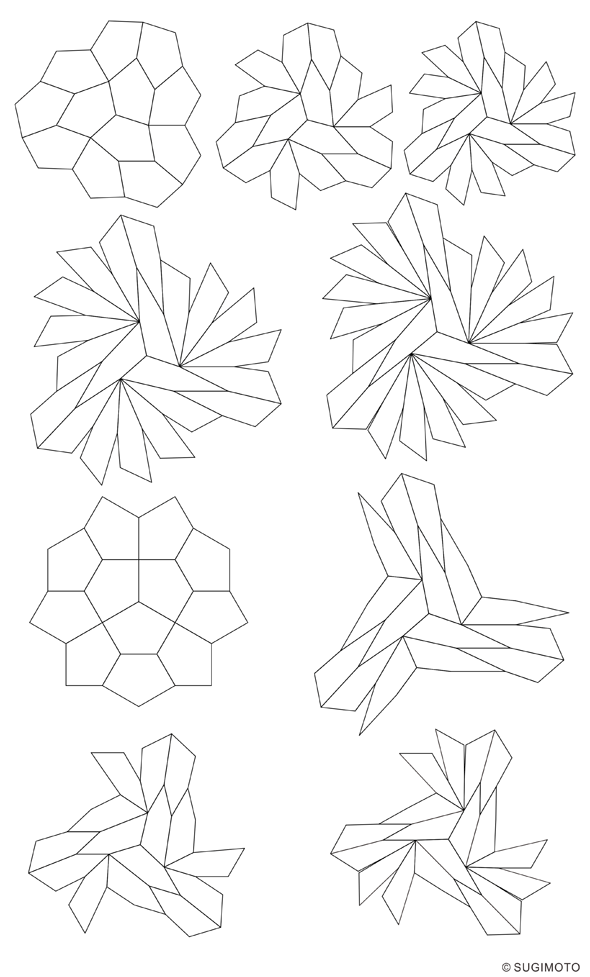
このことを踏まえて以下のような問題を考えてみました．

「タイルTが凸形で自身の合同なコピーで1回だけ囲める場合（つまり，TはHeesch数が1である凸形タイルの場合），3個のそのタイルの集団を自身の合同なコピーで1回だけ囲むことができるようなタイルTは存在する．4以上の整数kに関して，k個のタイルTの集団を自身の合同なコピーで1回だけ囲むことができるようなHeesch数が1である凸形タイルTは存在するか？また，kの最大値は何か？」

ちょっとマニアックすぎる問題かもしれません．

メモ（現在の進行状況など）

球面の充填・被覆の問題

「単位球面上にN個の大きさの等しい球帽（球面上の円）を重ならないように配置したい．球帽の最大角直径を求めよ．最大を与えるときの球帽の配置はどのようなものか？また，そのような的に一通りか？」をTammesの問題（球帽を用配置は本質いた単位球面の最密充填問題）と呼びます．この問題は， N = 1, ..., 14, 24に関してのみ数学的証明を伴った最適解が与えられています．

ここで，角半径 r の球帽に対して，角半径を半分の r/2 にした球帽を半球帽と呼ぶことにします．私は球帽中心が他の球帽内部に存在しないという条件下で，球帽を用いた球面の逐次被覆を行いました．球帽中心が他の球帽内部に存在しないという条件を満たす球帽の球面被覆ならば，それらの球帽を同心の半球帽に置き換えると，半球帽は互いに重なりません．したがって私の球帽の逐次被覆法は，半球帽の球面充填と密接に関連します．

私の球面逐次被覆で の場合を求めた結果，本手法による解とTammesの問題の解が完全に対応しているという興味深い事実を見いだしました．特にN= 10に関して，いままでDanzerによって球帽の角直径が[1.154479, 1.154480]と近似値範囲のみで示されていましたが，私は初めて正確な値を数式で表しました（私の論文の「Packing and Minkowski Covering of Congruent Spherical Caps on a Sphere, II: Cases of N = 10, 11, and 12」や「Exact Value of Tammes Problem for N=10」を参照）．

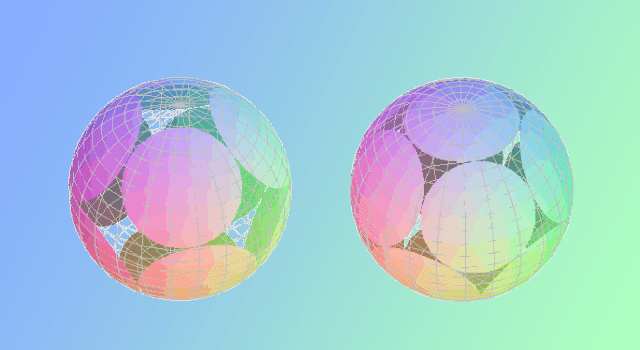
8回対称ペンローズ・タイリングのグラフ測地線を用いた解析

準結晶は，結晶とは違い周期性を持たない構造なので2次元・3次元においてはなおさら様々な角度からの特徴づけが必要となります．そこで，一般の２次元三角形網を特徴づけるものとして小川・ Collinsが導入したグラフ測地線という方法を用いて，８回対称ペンローズ・パターンの解析を試みました．