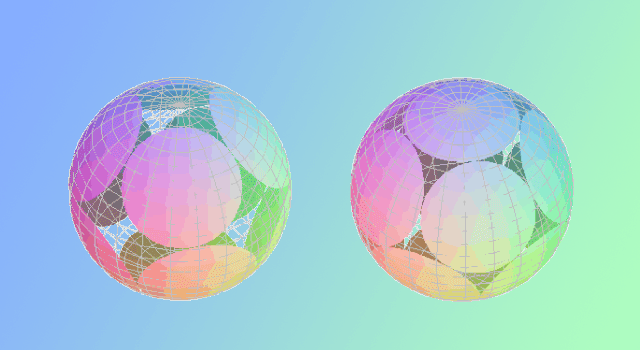Convex pentagonal tiling problem

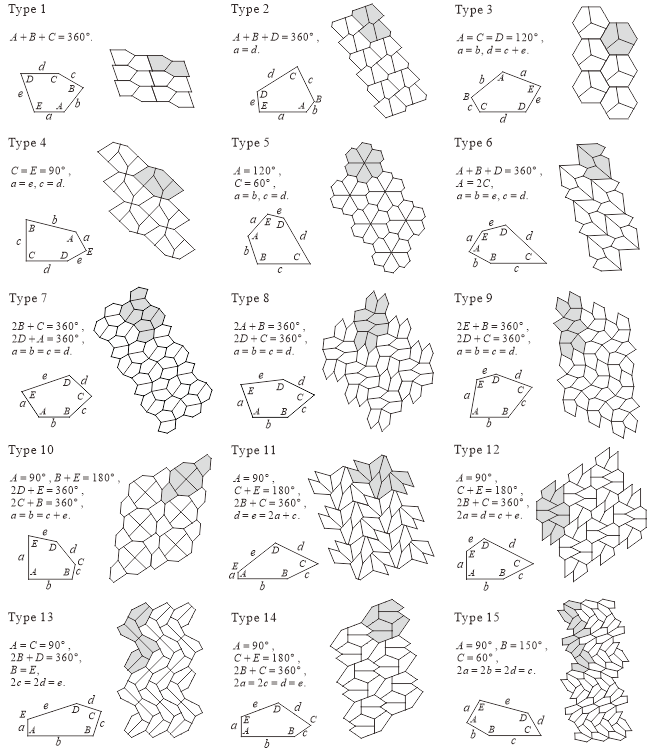
Tiling refers to coverage of the plane with polygons (tiles) without gaps or overlapping, and a single congruent polygon that tiles a plane is called a polygonal tile. Plane tiling with convex polygons has primarily been studied in an attempt to exhaust all the possible shapes that can tile a plane by a single congruent element. As to polygonal tiles, it is known as following. All triangles and quadrilaterals tile the plane. The convex hexagon that is tileable can be categorized into three families. In the cases of convex polygons with seven or more edges, no polygonal tiles exist. The classification problem of convex pentagons that can tile the plane is still open and is generally termed the convex pentagonal tiling problem. Now, known convex pentagonal tiles at present are classified into 15 families.

I collected all types about convex pentagons (convex pentagonal tile) that can generate an edge-to-edge tiling. （See my papers "Convex Pentagons for Edge-to-Edge Tiling, III" or "Tiling Problem: Convex Pentagons for Edge-to-Edge Monohedral Tiling and Convex Polygons for Aperiodic Tiling."）

Convex pentagons with Heesch number

In 2015, I intensively studied a convex pentagon whose Heesch number is finite. This research has not ended yet, but I have created one paper.

Wikipedia: Heesch's problem

Yoshio Agaoka; An example of convex heptagon with Heesch number one

Craig S. Kaplan; Heesch Numbers, Part 4: Edge-to-Edge Pentagons

Packing and covering on spherical surface

“How must N congruent non-overlapping spherical caps be packed on the surface of a unit sphere so that the angular diameter of spherical caps will be as great as possible?” This packing problem is also called the Tammes problem and mathematically proved solutions were known for N = 1, ..., 14, and 24.

On the other hand, the problem “How must the covering of a unit sphere be formed by N congruent spherical caps so that the angular radius of the spherical caps will be as small as possible?” is also important. It can be considered that this problem is dual to the problem of packing of Tammes. Among the problems of packing and covering on the spherical surface, the Tammes problem is the most famous. However, the systematic method of attaining these solutions has not been given.

We considered the covering in connection with the packing problem. As to N = 2,... 12, we found out that the solutions of our sequential covering and the solutions of the Tammes problem were strictly correspondent. Especially, we succeeded to obtain the exact closed form for N = 10. (See our papers "Packing and Minkowski Covering of Congruent Spherical Caps on a Sphere, II: Cases of N = 10, 11, and 12" or "Exact Value of Tammes Problem for N=10.")