数学セミナーの誤植

2016年1月号の数学セミナーで「平面タイル張り可能な凸五角形」という記事を書かせてもらいましたが，45頁の図1の凸五角形タイルの条件でいくつかの編集による誤りがみつかりました．該当箇所は，

type 2の「A+B+C = 360°」は「A+B+D = 360°」の誤り，

type 6の「A+B+C = 360°」は「A+B+D = 360°」の誤り，

type 15の「2a = 2b = 2d = e」は「2a = 2b = 2d = c」の誤り，

です．

数セミは送られた原稿にある複雑な数式を一から打ち直す（組み直す）そうです．図は雑誌全体の統一を図るためトレースして文字も調整しするそうです（図内の数式は組み直しも適用されるようです）．

現在主に進行中

Edge-to-edgeタイル張り可能な凸五角形の研究を利用して，Heesch数を持つ凸五角形の調査．

回転対称なタイリング．

その他の課題

凸六角形タイルが3つのtypeに分類できることの証明（現在，この事実は認識しているがその証明は未確認． Reinhardtの証明はドイツ語のため簡単には確認できていないが， 中国人の研究者の論文によるとedge-to-edgeタイル張りを前提としているという話もある．ただし，後のBollobasの研究で凸六角形タイルの分類の結果は 保証されているという話も書かれている．この件に関して，自分なりの証明方法を一応考えているが，多くのパターンを確認する必要あり，短時間ではそれを やり遂げるのは現状では難しいと考えている）．

7辺以上の凸多角形がタイリング生成不可能である（7辺以上の凸多角形タイルが存在しない）証明

Grünbaum and ShephardのTILINGS AND PATTERNS (W. H. Freeman and Company, New York, 1987)にこの結果に該当する話は当然あるのですが，そのものずばりの記載になっていないためちょっとわかりにくいかもしれません（その内容は，適用範囲がタイルを凸多角形に限定しないでものになっている．そのため証明もそれほど簡易ではない）．代わりに，

M.S. Klamkin and A. Liu, Note on a result of Niven on impossible tessellations, American Mathematical Monthly, 87 (1980) 651--653.

が内容も短く，わかりやすいと思われます．

以前は，このことに関する証明をなにかしらのかたちで発表しようと思っていましたが，上記の論文はWebから取得も容易な環境（Googleの検索で見つかります）にあることから，あえて私が示すこともないと思っています．

印のない一種類の合同な凸多角形によるp3m1のタイリング

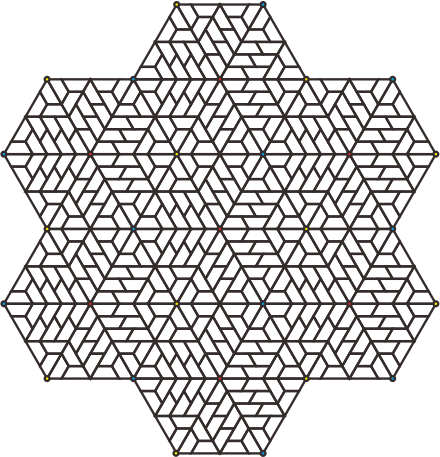
平面の結晶群（模様群）は17種（17 wallpaper groups)に分類されます．その中のp3m1のタイリングを，印のない一種類の合同な凸多角形で形成する方法はある？と以前とある方に質問されました．私はわからなかったのですが，このことをJaap Scherphuis氏に聞いてみたところ，正三角形を台形で12分割するものを用いて形成する方法を教えてもらいました．その方法で私が作成したタイリングが下図です．ただし，下記のタイリングはたしかにp3m1タイプなのですが，印がある正三角形（12個の台形に等分割された模様の正三角形）タイルのp3m1タイプのタイリングと見なすのが適切だと思うようになりました．

タイリングの対称群がタイル全体の集合に推移的に作用するものを「Isohedral」と呼び，k個（k>=2）の推移的作用があるタイリングを「k-isohedral」と呼ぶことにします．印のないタイルでp3m1のisohedralタイリングは生成できないと知られています．下図の台形のタイリングは12-isohedralですが，このタイリングを台形で考えると「どの120度回転の中心にもそれを通る鏡映軸がある」というp3m1のタイリングが満たすべき性質にあわない箇所があります．したがって，下記の台形のタイリングは，印のないタイルを用いたp3m1のk-isohedralタイリング（k>=2）とはいうよりは，印のあるタイルを用いたp3m1のisohedralタイリングと見なすのが適切だと考えました．

下記の台形のタイリングとは違って，「無印のタイルを用いたp3m1の（性質から外れる箇所がないような）k-isohedralタイリング（k>=2）は存在するのか？」ということになるのですが，そのようなものは現在知られていないと思われます．なお，Japp氏はk<=6ではそのようなものはないのではないかと言っています（証明はないそうです）．

過去データ・メモ置き場

• 凸五角形とテセレーション （ エッシャー生誕121年記念テセレーション講演会，東京都美術館，2019年6月15日）.

• Heesch数が正となる凸五角形 （第87回形の科学シンポジウム， 東京慈恵会医科大，2019年6月8日）.

• アートパズル展・浜田市世界こども美術館（2019年3月28日～5月26日）．

•　図形と空間の不思議～敷き詰め模様で遊ぼう～・サイエンスアゴラ2018（2018年11月10日～11日）．

•　五角形パズルの常設展示, はまぎん こども宇宙科学館, 2018年11月1日．

•　Heesch数が正となる凸五角形（タイリングと準周期系の周辺，京都大学数理解析研究所，2018年10月15日）.

•　企画展：＜期間限定展示＞五角形パズル, はまぎん こども宇宙科学館, 2018年7月21日～9月2日．

•　万能タイルを敷きつめよう！ ～TH-五角形のパズルに挑戦～, 多摩六都科学館, 2018年3月20日～3月31日．

•　Heesch数が正となる凸五角形（直観幾何学2018，椙山女学園大学，2018年2月17日）．

•　図形と空間の不思議 - 敷き詰め模様で遊ぼう!・サイエンスアゴラ2017（2017年11月25日～26日）．

•　凸五角形タイリングとヘプタモンド（タイリングと準周期系の数理，京都大学数理解析研究所，2017年10月17日）.

•　凸五角形を用いたタイル張り（第24回 沼津研究会，沼津工業高等専門学校，2017年3月7日）．

•　凸五角形タイリングとヘプタモンド（直観幾何学2017，熊本大学，2017年2月11日）．

•　凸五角形とタイル張り（龍谷大学数理情報学科特別講義，2016年11月23日）．

•　図形と空間の不思議 - 敷き詰め模様で遊ぼう!・サイエンスアゴラ2016（2016年11月3日～6日）．

•　凸五角形（Rice1995）を用いて形成できるタイリング（第82回形の科学シンポジウム，2016年10月8日）．

•　はまぎん こども宇宙博物館 特別企画「しきつめの世界展～エッシャーからテセレーションへ～」に出展（2016年9月25日～2016年10月30日）．

•　はまぎん こども宇宙博物館 特別企画「しきつめの世界展～エッシャーからテセレーションへ～」に出展（2016年7月19日～2016年8月31日）

•　平面タイル張り可能な凸五角形（直観幾何学2016，熊本大学，2016年2月7日）．

•　凸五角形による周期的タイリングに関する考察（第77回形の科学シンポジウム，2014年6月14日）．

•　凸五角形のEdge-to-Edgeタイリングと凸多角形の非周期的タイリング（2012年度応用数学合同研究集会，2012年12月22日）．

•　Edge-to-Edgeタイル張り可能な凸五角形と非周期的Edge-to-Edgeタイル張り可能な凸多角形（第74回形の科学シンポジウム，2012年11月18日）．

•　Edge-to-edgeタイル張り可能な凸五角形タイルの分類と非周期的edge-to-edgeタイル張り可能な凸多角形の性質（研究集会・タイリング空間のトポロジーとその周辺，京大数理研，2012年10月4日）．

•　Edge-to-edgeタイル張り可能な凸五角形と非周期的edge-to-edgeタイル張り可能な凸多角形（東海大，2012年3月22日）．

edge-to-edgeタイル張り可能な凸五角形タイルのtypeの網羅が完了（2012年2月13日）．

プライバシーポリシー

サイトの利用状況を解析するためにGoogleアナリティクスを用いており，Googleアナリティクスはクッキー情報を利用して利用者の情報を収集しています．収集したデータは，利便性の向上や統計データの取得のために用いられています．これらのデータは匿名であり，個人情報（氏名・住所・生年月日などの情報）は含まれていません．

Googleアナリティクスの利用規約に関する説明については

Google Analyticsのポリシーと原則　http://www.google.com/intl/ja/policies/

をご覧ください．このようなデータ収集を拒否（オプトアウト）したい場合は，使用しているブラウザにてクッキーの拒否を選択してください．設定方法は，各ブラウザのヘルプを参照していください．